
Solved Solve Th 1 Elimination 2x Y 5 3x Y 10 E Chegg Com
NCERT Solutions for Class 10 Maths Chapter 3 Exercise 34 Question 1 Summary On solving the pair of equations by the elimination method and the substitution method we get x, y as (i) x y = 5 and 2x 3y = 4 where, x = 19/5, y = 6/5 , (ii) 3x 4y = 10 and 2x 2y = 2 where, x = 2, y = 1 , (iii) 3x 5y 4 = 0 and 9x = 2y 7 where, x = 9/13, y = 5/13, (iv) x/2 2y/3 = 1 and x y/3 To solve the system of equations, use elimination The equations are in standard form and the coefficients of m are opposites Add { n m = 39 n − m = 9 _ 2 n = 48 Solve for n n = 24 Substitute n=24 into one of the original n m = 39 equations and solve form 24 m = 39 m = 15 Step 6 Check the answer
The elimination method calculator
The elimination method calculator-Hence, Solution is x=2 , y=−3 By Substitution Method Expressing x in terms of y from equation (i), we have x= 3−6−4y Substituting the value of x in equation (ii) from equation (i), we get 3×( 3−6−4y )−y=9 ⇒−6−4y−y=9 ⇒−6−5y=9 ⇒−5y=96=15 ∴y= −515Web & Mobile subscription

Show Graphically That The System Of Linear Equations 2x 3y 5 6y 4x 3 Youtube
We have two linear equations (to be solved by elimination method) 3x −4y = 9 2x 3y = 7 Multiply first eq by −2 and second by 3 −6x 8y = −18 6x 9y = 21 Now we can add both equations and eliminate the unknown x 17y = 3 y = 3 17Suggested Method Reason 5x y = 32 y = x 2 Substitution The value of y can be substituted into the first equation 4x – 3y = –13 7x 3y = –9 Elimination 3y and –3y are opposites and can easily be eliminated using addition 8x 3y = –7 4x y = 4 Elimination y can be eliminated by multiplying the second equation by –31 12x 5y = 7 and 2x 3y 5 = 0 2 x y = 2 and 2x 3y = 4 3 7y 2x 11 = 0 and 3x y 5 = 0 4 3x y 5 = 0 and 2x 7y 11 = 0 5 3x y = 3 and 7x 2y = 6 2x y = 11 and 5x 4y = 1 7 2x 7y = 1 and 4x 3y = 15 8 3x 5y = 1 and 5x 2y = 19 9 5x 8y = 9 and 3y 2x = 4 10 6x 5y = 2 and 5x 6y = 9
Best answer The given equations are 3/x 1/y 9 = 0, ⇒ 3/x 1/y = 9 (i) ⇒ 2/x 3/y = 5 (ii) Putting 1/x = u and 1/y = v, we get 3u – v = 9Step1 The first step is to multiply or divide both the linear equations with a nonzero number to get a common coefficient of any one of the variables in both equations Step2 Add or subtract both the equations such that the same terms will get eliminated3 x 4 y = 9 1 Total value 3 x 2 y = 9 2 add (1) & (2) 2y=18 /2 y=9 plug y in (1) 3x4y=9 3x4(9)=9 3x36=9 3x=27 /3 x=9
The elimination method calculatorのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
「The elimination method calculator」の画像ギャラリー、詳細は各画像をクリックしてください。
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning | Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
「The elimination method calculator」の画像ギャラリー、詳細は各画像をクリックしてください。
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
「The elimination method calculator」の画像ギャラリー、詳細は各画像をクリックしてください。
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning | Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
「The elimination method calculator」の画像ギャラリー、詳細は各画像をクリックしてください。
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning | Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning | Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
「The elimination method calculator」の画像ギャラリー、詳細は各画像をクリックしてください。
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning | Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning | Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
「The elimination method calculator」の画像ギャラリー、詳細は各画像をクリックしてください。
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning | Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
「The elimination method calculator」の画像ギャラリー、詳細は各画像をクリックしてください。
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning | 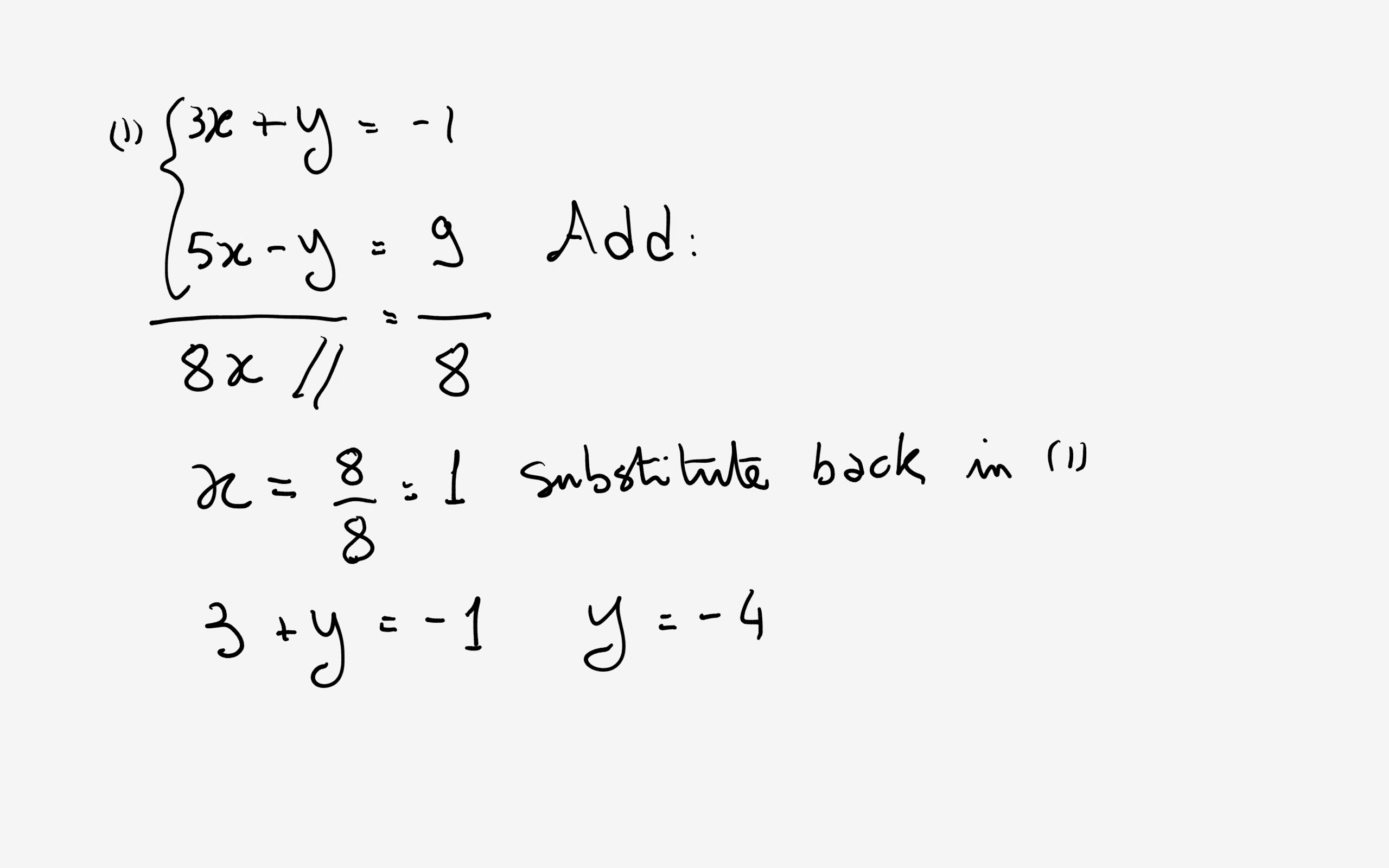 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning | 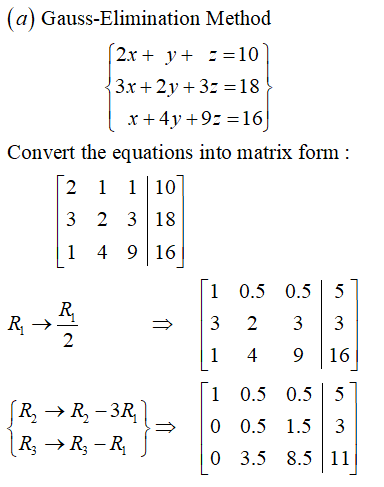 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
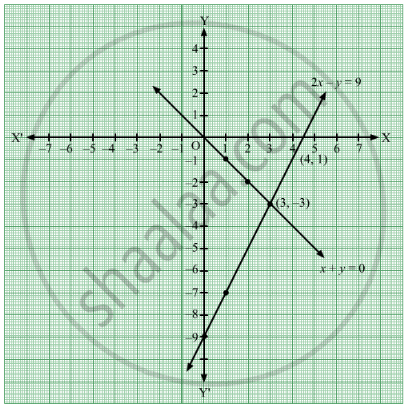 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning | Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
「The elimination method calculator」の画像ギャラリー、詳細は各画像をクリックしてください。
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning | Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
「The elimination method calculator」の画像ギャラリー、詳細は各画像をクリックしてください。
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
「The elimination method calculator」の画像ギャラリー、詳細は各画像をクリックしてください。
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning | Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
「The elimination method calculator」の画像ギャラリー、詳細は各画像をクリックしてください。
Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
 Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |  Rd Sharma Solutions For Class 10 Mathematics Cbse Chapter 3 Pairs Of Linear Equations In Two Variables Topperlearning |
We have to solve for x and y in the given equations by the elimination method 3x – 5y = 4 (1) 9x – 2y = 7 (2) On multiplying eq (1) by 3, we get 9x – 15y = 12 (3) Now we can easily subtract (2) and (3) to get – 9x – 15y = 12Free system of equations elimination calculator solve system of equations unsing elimination method stepbystep
Incoming Term: elimination method with 3 equations, elimination method calculator mathway, elimination method 3 equations calculator, how to solve by the elimination method, solve by the elimination method calculator, solve equation by elimination method, elimination method step by step calculator, the elimination method math, algebra solve by elimination method, elimination method algebra 1, the elimination method calculator, elimination method algebra calculator,




0 件のコメント:
コメントを投稿